許多時候離散機率不足以表達生活中常見的情境，比如說估算一個不規則形狀的面積、或是均勻地選擇一個介於 0 與 1 之間的小數等等。這時候我們需要將機率分佈的定義拓展到連續機率空間，許多有趣的現象應運而生。

約瑟·伯特蘭 (Joseph Bertrand, 1822-1900)，法國數學家，有相當多的數學成果流於後世。筆者最喜歡的是他提出關於質數的重要猜想 (Bertrand's Postulate)：任何大於 3 的正整數 n，在 n 與 2n 之間至少存在一個質數。不過今天要討論的是他在機率方面提出的貢獻：伯特蘭悖論 Bertrand's Paradox。

悖論的問題敘述是這樣子的：『在一個單位圓 (unit circle) 內隨機選擇一條弦 (chord)，這條弦的長度與圓內接正三角形的邊長比起來，較長的機率為何？』Bertrand 指出，「隨機選擇一條弦」這一句話其定義是相當模糊的。他並且給出三種選擇隨機弦的方式：其一、在圓周上均勻地隨機選擇兩個點，並將兩點相連為弦。其二、使用極角座標 (r, θ)，均勻挑選弦心到圓心的半徑 r 以及傾角 θ。其三、隨機在圓內選擇一個點，以該點為弦心定義出來的弦。這三種方式最後得到的結果都不相同。

我們可以將這三種取樣方式得到的弦長寫成函式：

def random_chord_by_two_points():
    t1 = np.random.uniform(0.0, 2*np.pi)
    t2 = np.random.uniform(0.0, 2*np.pi)
    p1 = np.array([np.cos(t1), np.sin(t1)])
    p2 = np.array([np.cos(t2), np.sin(t2)])
    return np.linalg.norm(p2-p1, ord=2)

def random_chord_by_radius():
    r = np.random.uniform(0.0, 1.0)
    return 2 * np.sqrt(1 - r*r)

def random_chord_by_inner_point():
    r = np.random.uniform(0.0, 1.0)
    return 2 * np.sqrt(1 - r)

然後就可以跑個 10000 次實驗並查看弦長有多少機率比圓內接正三角形邊長還長囉～

N = 10000  # 設定模擬次數。

x0 = np.sqrt(3)
plt.axvline(x = x0, color = 'k', alpha=0.7, linestyle='dashed', label = '單位圓內接正三角形邊長')
ax = plt.gca()
ys = np.linspace(0, 1, N+1)[1:]

def add_plot(sampling_method, label):
    arr = [sampling_method() for _ in range(N)]
    arr.sort()
    y0 = bisect.bisect_left(arr, x0) / N
    color = next(ax._get_lines.prop_cycler)['color']
    plt.plot(arr, ys, label=label, color=color)
    plt.plot(x0, y0, marker='o', linestyle='none', alpha=0.7, markersize=10, color=color)
    
add_plot(random_chord_by_two_points,  '1. 圓周上選兩點')
add_plot(random_chord_by_radius,      '2. 半徑與角度')
add_plot(random_chord_by_inner_point, '3. 圓內一點')

plt.title('經過模擬得出的累積分佈函數 ECDF', fontname='LiHei Pro', fontsize=18)
plt.legend(loc='upper left', prop=font)
plt.xlabel('弦長', fontname='LiHei Pro', fontsize=12)
plt.ylabel('累積機率', fontname='LiHei Pro', fontsize=12)
plt.show()

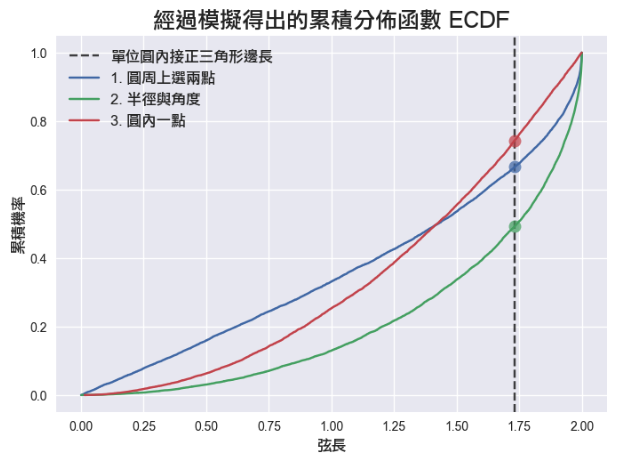
上述顯示模擬後的結果，與理論值 (第一種方法是 1/3、第二種方法是 1/2、第三種方法是 1/4) 大致吻合～